Aho-Corasick法をしっかりと理解する話

はじめに

個のキーワード が定められている環境下で、入力テキスト からそれらの出現位置を全列挙するクエリを考えます。

文字列の一致判定はローリングハッシュなどを用いて定数時間でできるにしても、含まれている場所が分からない以上は、テキスト1つあたり 程度の計算量になってしまいそうです。

Aho-Corasick法は、キーワードに対して で工夫したTrie木を作る*1ことで、クエリあたり で処理できます。強い。*2

本記事は、Aho-Corasick法の考え方やざっくりとしたアルゴリズム、計算量評価の方法をまとめたものです。これを読めば、Aho-Corasick法をしっかりと理解でき、自力で実装できるようになる…かも？

この記事でやること

Aho-Corasick法をできる限り丁寧に解説します。

また、最後にPython(PyPy)での実装例を載せてあるので、ご自由にお使いください。

Aho-Corasick法の解説

Trie木を効率よく辿る

まずキーワードでTrie木を作っておきます。

【図1】 のTrie木

このTrie木において、 の 文字目（以後、 と表記、0-indexedとする。）を左端とするキーワードを見つけたい場合、

• Trie木の根に"駒"を置き、 とする。
• 駒のいるノードに文字 の枝が存在する限り、その先のノードに駒を進めて をインクリメントすることを繰り返す。

とすればよいです。

具体例として、 として考えてみましょう。

【図2-1】 に対し、左端を とするキーワードを見つけたい。

【図2-2】、キーワード を発見！

しかし、これを各左端について行うと になるので、まだまだ嬉しくありません。

Aho-Corasick法では、この左端の切り替えを効率よく行います。

試しに、【図2-2】の続きを考えてみましょう。

今、 の枝が駒のいるノードに存在しないため、駒を進めるループを脱出した状態です。なので、次は駒を根に戻し として再度駒を進めるループに入ります。

このループは と駒を進めますが、この と進める部分は、前回のループで と進めたことを思い出すと無駄な動きをしているような気がします。どうせなら根に戻らず直接 のノードに移したいですね。

【図3】駒を から直接 に移したい

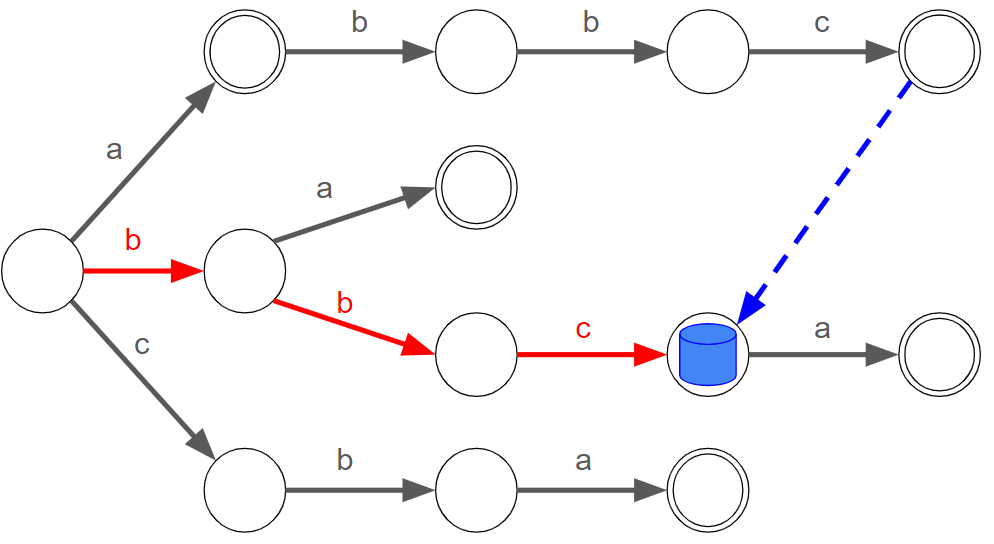
これを一般的に述べます。

便宜上、根から駒がいるノードまでのパスにより得られるテキストを読み込んでいるテキストと呼ぶことにします。

ループが止まった後の駒の移動先は、「読み込んでいるテキストの接尾辞（自身は除く）であって、キーワードの接頭辞として含まれる最長のもの」を表すノードとすればよいです。（なので、 で止まったあと駒は に移動します。）

Trie木の構造上、根以外のどのノードに駒があったとしても対応した上記の移動先のノードが一意に定まります。そこで、各ノード について対応する移動先のノードを と表すことにしましょう。根以外の全てのノードに対して が既に求まっているものと仮定すると、ざっくり次のような手順で全てのキーワードを列挙できます：

• 駒をTrie木の根に置き、 に対して、順に以下を行う:
  
  • 駒がいるノードが根でなく、かつ文字 の枝が存在しない限り、駒を に移すことを繰り返す。
  • 駒がいるノードに の枝が存在するなら、その先のノードに移す。
  • 読み込んでいるテキストの接尾辞として含まれるキーワードを列挙する。（※）

この手順で全てのキーワードが過不足なく列挙できていることは、（※）の操作によって を末尾とするキーワードが全て列挙されていることから分かります。

列挙の方法としては、 を根に到達するまで辿り、キーワードそのものになっているものを抽出すればよいです。さらに、 を適切に経路圧縮して得られる「読み込んでいるテキストの接尾辞（自身は除く）として含まれる、最長のキーワード」を表すノードへの辺を用意しておけば、計算量を出現回数で抑えられます。*3

ここで、次のスライドショーを見てもらうとわかる通り、読み込んでいるテキストは駒の移動に合わせて常に右方向に動きます。つまり、尺取法の要領で駒の移動回数が高々 回に抑えられるわけですね。

ということで、あとは各ノードに対する を前計算するパートを倒せばよいです。

fail の前計算

の定義を思い出すと、 の移動先のノードはTrie木において自身より浅い位置にあります。そこで、 について深さ 以下の全てのノードの が求まっていると仮定して、深さ のノード について を求め方を考えます。また、便宜上 としておきます。

の親を とします。また、根から までのパスによるテキストを 、 から文字 の枝を通って に到達するものとします。

が指すノードは、「 の接尾辞（自身は除く）であって、キーワードの接頭辞として含まれる最長のもの」を表すノードでした。これは必ず の接尾辞に をつけた形をしている点に注意すると、次の手順で を求めることができます：

• とする。
• が根でない かつ が の枝を持たない限り、 とすることを繰り返す。
• が の枝を持つなら とする。そうでないなら、 とする*4。

そして、根から始めるBFSにて を見るときに、各子ノード に対して、上記の処理をしたのちにキューに入れていくことで、全てのノードの を求めることができます。

計算量を考えてみましょう。BFS部分は でいいとして、 を求めるループが問題です。実は、各キーワード について、 の各文字のノードによるループの合計回数が高々 回で抑えられます（※※）。よって、前計算全体で となります。

（※※）の証明

キーワード について、「 の接尾辞（自身は除く）であって、キーワードの接頭辞として含まれる最長のもの」の長さを とし、 の末尾 文字による文字列を とします。次に、 から末尾の を削った部分文字列対して同様の操作を行い と を得ます。以下これを繰り返して 、 が得られたところで となったとします。また、、 とします。

このとき、各 について、 の各文字のノードの　 を求めるループは高々 回で抑えられます。なぜなら、

• のノードについては、親ノードの 移動先の深さが であることに注意すると、高々 回のループで求まる。
• のノードについては、親ノードの 移動先のノードに必ず の枝が存在するため、ループは1回しか発生しない。

となるからです。

競プロへの応用

冒頭で示したような列挙クエリは、計算量的に競プロではおそらく問われません。

そこで、列挙の代わりに各キーワードの出現回数を数え上げる問題を考えてみましょう。

単純なのは、各キーワードがそれぞれ何回出現したかを表す配列を用意して、前述の（※）を利用してインクリメントしていくという方法です。しかし、これでは計算量が変わらず出現回数に依存してしまいます。

解決法としては、各ノードについて（※）が始まるノードになった回数をカウントしておき、最後に木dpの要領で、回数を に沿って配りつつキーワードの末尾ノードに到達するごとにその値を配列に加算していけばよいです。

問題例 ↓

atcoder.jp

Pythonでの実装例

• PyPy3.10-v7.3.12 にて動作確認済。

from collections import deque
sys.setrecursionlimit(200000) # enum() を使わないならコメントアウトしてOK。
class AhoCorasick_Node:
    def __init__(self, a=None) -> None:
        self.a = a
        self.son = {}
        self.fail = self
        self.output = None
        self.nxt_output_node = self
        self.dp = 0
    
    def find_nxt(self):
        if self.nxt_output_node is self:
            return self
        if self.nxt_output_node.output is None:
            self.nxt_output_node = self.nxt_output_node.find_nxt()
        return self.nxt_output_node

class AhoCorasick:
    def __init__(self, words) -> None:
        self.words = words
        self.head = AhoCorasick_Node()
        self._build_Trie()
        self._set_fail()

    def _build_Trie(self):
        for w_idx, word in enumerate(self.words):
            node = self.head
            for a in word:
                if a not in node.son:
                    node.son[a] = AhoCorasick_Node(a)
                node = node.son[a]
            node.output = w_idx

    def _set_fail(self):
        dq = deque([self.head])
        while dq:
            now = dq.pop()
            for a, nxt in now.son.items():
                node = now.fail
                while a not in node.son and node.fail is not node:
                    node = node.fail
                if a in node.son and node.son[a] is not nxt:
                    nxt.fail = node.son[a]
                else:
                    nxt.fail = self.head
                nxt.nxt_output_node = nxt.fail
                dq.appendleft(nxt)
    
    def enum(self, text):
        node = self.head
        ret = [[] for _ in range(len(self.words))]
        for i, a in enumerate(text):
            while a not in node.son and node.fail is not node:
                node = node.fail
            if a in node.son:
                node = node.son[a]

            if node.output is not None:
                w_idx = node.output
                ret[w_idx].append(i+1-len(self.words[w_idx]))
            output_node = node
            while output_node.find_nxt() is not self.head:
                output_node = output_node.nxt_output_node
                w_idx = output_node.output
                ret[w_idx].append(i+1-len(self.words[w_idx]))

        return ret
    
    def cnt(self, text):
        tps = []
        dq = deque([self.head])
        while dq:
            now = dq.pop()
            now.dp = 0
            tps.append(now)
            for nxt in now.son.values():
                dq.appendleft(nxt)

        node = self.head
        ret = [0]*len(self.words)
        for a in text:
            while a not in node.son and node.fail is not node:
                node = node.fail
            if a in node.son:
                node = node.son[a]
            node.dp += 1

        for node in reversed(tps[1:]):
            if node.output is not None:
                w_idx = node.output
                ret[w_idx] += node.dp
            node.fail.dp += node.dp
        return ret

使用例↓

Submission #56078430 - Toyota Programming Contest 2024#7（AtCoder Beginner Contest 362）

ちなみに

これは驚愕の事実なのですが、Aho-Corasickは 「えいほこらしっく」であって、「あほこらしっく」ではないそうです。

エイホ–コラシック法 - Wikipedia

参考文献

1. Aho Corasick 法 - naoyaのはてなダイアリー

2. Alfred V. Aho and Margaret J. Corasick. 1975. Efficient string matching: an aid to bibliographic search. Commun. ACM 18, 6 (June 1975), 333–340.

*1:正確に述べると、これは内部のTrie木でハッシュテーブルを用いた場合の期待計算量になっています。配列でTrie木を作る場合は文字種数σ倍かかるかわりに最悪計算量になります。どちらで実装するかはお好みでどうぞ。

*2:なお のようなケースを考えれば出現回数を壊せるので、競プロ目線では出現回数に依存しないクエリを考えることが多そうです。

*3:経路圧縮のために余分に潜る操作は、高々Trie木のノード数回しか発生しないため、Trie木構築時の計算量に押しつけて"ならす"ことができます。

*4:この場合での は必ず根になります。そこで、根について本来存在しない文字の枝を全て自身へのループとしておけば、ここの場合分けをなくすこともできます。