次回 >>
はじめに
競プロをのほほんとやりながら大学生活を過ごしてきましたが、実は大学を卒業するには卒論とかいうものを書かないといけないらしいです。困りました…。
一応ざっくりとやりたいことは決まってて、それをやる武器としてどうやら「ZDD」とかいうデータ構造が使えそう（な気がする）（使ってみたらどうなるかな？くらいの気持ち）なので、しばらくそれのお勉強をします。
せっかくなので、お勉強したことをブログにまとめていきたいと思います。やる気が続けば。
この記事でやること
・ZDDの解説と、各種演算のPython3.11による実装
・ZDDを用いて8-Queen problemを解く。
ZDD(Zero-suppressed Binary Decision Diagram, ゼロサプレス型二分決定グラフ)
ZDDとは？
ZDDは、与えられた集合（台集合 ）に対しその部分集合族を表現するデータ構造です。
特に、台集合に対しある種の条件を満たす部分集合のことを組合せ集合 と呼び、ZDDはこの組合せ集合全体を表現するのによく用いられます。例えば「ナップサック問題 の重量制限に収まる商品の集合全体」とか、「グラフ上のs-tパス全体」とかですね。
どうやって表現するの？
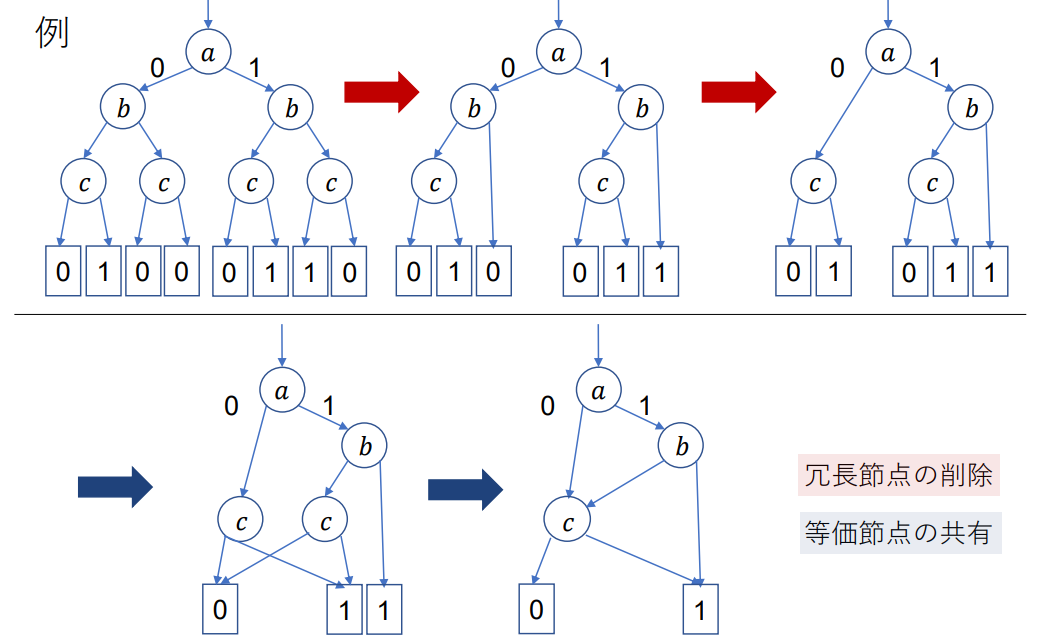
（各画像は [3] より引用）
台集合を
まず、以下の手順で Binary Decision Tree (二分決定木) を構築します。（長いので、クソデカ木 と呼称することにします）：
高さ 0-枝 、1-枝 と呼ぶ。
木なので、葉を1つ選ぶと根からその葉までのパスが一意に定まる。このとき「
クソデカ木。台集合の要素が
クソデカ木は明らかに
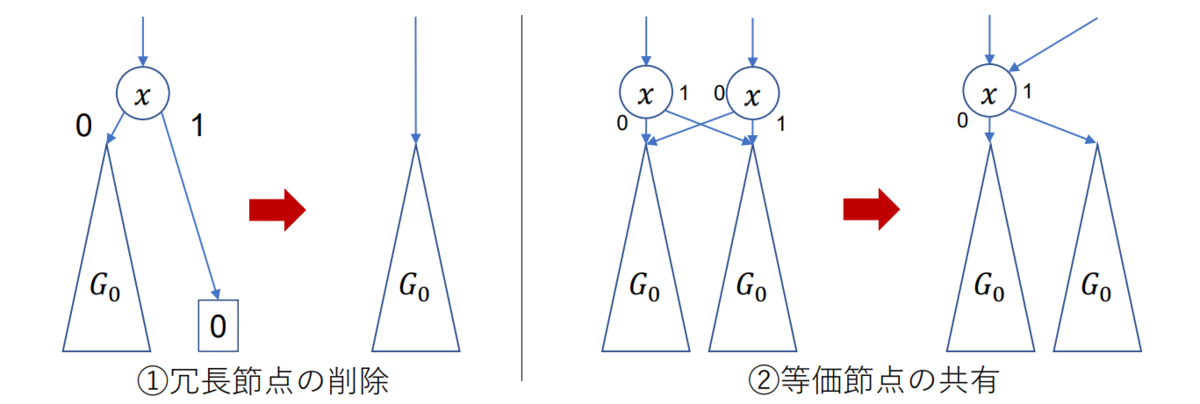
ZDDは、クソデカ木に対し以下の2種の操作を可能な限り繰り返すことでノードを削減したものとなります*1 ：
冗長接点の削除
1-枝が0の値を持つ葉を指している場合に、この節点を取り除き、0-枝の行き先に直結させる。
等価接点の共有
等価な節点（ラベルが同じで、0-枝同士，1-枝同士の行き先が同じ）を共有する。
※特に、葉は False/True それぞれ1つにまとめ、それぞれ0-葉 （あるいは
ノード削減のイメージ図
実際にクソデカ木からZDDを構築する様子
ただ、この手順でZDDを構築しようとするのは、最初にクソデカ木を陽に作ることになるので実質不可能 です。悲しいね。
ではZDDをどう扱うかというと、部分集合族に対する様々な演算（和集合をとる など）をZDD上での操作で表現するというのが基本的な用法になります。
ここからは、具体的な実装を見ながらZDDの各種演算を解説していきます。
ZDDのプログラム上での表現方法と実装準備
まず実装上の前提として、ZDDクラス とDiagramクラス を分けて作ります。
ZDDクラスには基礎的な組合せ集合のDiagramを作る関数を用意し、Diagramクラスにメインとなる演算を書いていきます。
Diagramと言っても、インスタンス そのものはノードを表現します。このクラス名は、各ノードを根とする部分グラフによって小さな部分集合族が表現されていることを踏まえています。
また、ZDDインスタンス 上のハッシュテーブルにDiagramインスタンス を記録していく（正確にはDiagramインスタンス 生成する関数 _get_node() をメモ化する）ことで、全体として永続データ構造のように扱います。
ZDDクラスのコンストラク タ
*2
class ZDD :
def __init__ (self, ground_set, Diagram=Obsolete_Diagram) -> None :
self.idx = {v: i for i, v in enumerate (ground_set)}
self.idx[None ] = len (ground_set)
self.Diagram = Diagram
self.zero_terminal = self.Diagram(zdd=self)
self.one_terminal = self.Diagram(zdd=self)Diagramクラスのコンストラク タ、ハッシュ関数
インスタンス を表します。インスタンス を表します。ハッシュ関数 は、2つの葉については乱数で、そうでない場合はラベルと左右のDiagramインスタンス のハッシュ値 から計算します。これは、特に【等価節点の共有】に用います。Diagramのインスタンス に対し破壊的な処理を行うことはないので、コンストラク タ内で計算して
※ コードではObsolete_Diagramクラスとしています。
class Obsolete_Diagram :
def __init__ (self, zdd, top=None , zero=None , one=None ) -> None :
self.zdd = zdd
self.top = top
self.zero = zero
self.one = one
if top is None :
self.hash = randint(0 , 10 **9 )
else :
self.hash = (top, zero.hash, one.hash).__hash__()ZDDを図示する関数 Diagram.show(self, filename)
Diagramクラス で宣言します。pyvis を別途インストールし、from pyvis.network import Network する必要があります。filename は .html (HTML拡張子) である必要があります。
def show (self, filename):
"""
selfによるzddを図示
filemame: html拡張子のファイル名
"""
nodes = {self: 0 }
net = Network(directed=True )
dq = deque()
if self is self.zdd.zero_terminal:
net.add_node(nodes[self], shape="box" , label="⏊" )
elif self is self.zdd.one_terminal:
net.add_node(nodes[self], shape="box" , label="⏉" )
else :
net.add_node(nodes[self], shape="circle" , label=self.top.__repr__())
dq.appendleft(self)
while dq:
p = dq.pop()
if p.zero not in nodes:
nodes[p.zero] = len (nodes)
if p.zero is self.zdd.zero_terminal:
net.add_node(nodes[p.zero], shape="box" , label="⏊" )
elif p.zero is self.zdd.one_terminal:
net.add_node(nodes[p.zero], shape="box" , label="⏉" )
else :
net.add_node(nodes[p.zero], shape="circle" , label=p.zero.top.__repr__())
dq.appendleft(p.zero)
net.add_edge(nodes[p], nodes[p.zero], color="red" )
if p.one not in nodes:
nodes[p.one] = len (nodes)
if p.one is self.zdd.zero_terminal:
net.add_node(nodes[p.one], shape="box" , label="⏊" )
elif p.one is self.zdd.one_terminal:
net.add_node(nodes[p.one], shape="box" , label="⏉" )
else :
net.add_node(nodes[p.one], shape="circle" , label=p.one.top.__repr__())
dq.appendleft(p.one)
net.add_edge(nodes[p], nodes[p.one], color="blue" )
net.show(filename, notebook=False )
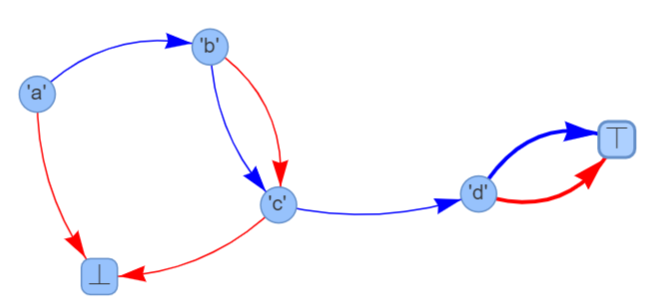
適当なインスタンス で実行すると、例えば下図のように表示されます。
図の見方は以下の通りです：
赤辺 ：0-枝青辺 ：1-枝
インスタンス ごとに関数をメモ化するデコレーター
グローバル に宣言します。Python では functools.cache を使えば関数をメモ化できますが、インスタンス ごとにテーブルを分けずに記録してしまうため、インスタンス をdelする際のメモリの解放が困難になります。（する方法があれば教えていただけると幸いです！）そこで、インスタンス ごとにテーブルを作ってそこにメモするようなデコレーターを作っておきます。使い方は functools.cache と全く同じです。
def cache (func):
"""
インスタンスメソッドをメモ化するデコレーター
"""
def _wrapper (self, *args):
if not hasattr (self, "_cache_table" ):
self._cache_table = {}
key = (func, args)
if key not in self._cache_table:
self._cache_table[key] = func(self, *args)
return self._cache_table[key]
return _wrapperDiagramインスタンス の生成に用いる関数 ZDD._get_node(self, v, zero, one)
ZDDクラス で宣言します。Diagramインスタンス 生成時に使い、2つの削除規則を漏れなく適用します。
【冗長接点の削除】は if 分岐で適用されます。
【等価節点の共有】は @cache によるメモ化で適用されます。
@ cache
def _get_node (self, v, zero, one):
if one is self.zero_terminal:
return zero
return self.Diagram(self, v, zero, one)
\begin{align} \mathcal{P}\text{.zero} & = \{C \mathrel{|} C \in \mathcal{P}, \mathcal{P}\text{.top} \notin C\} \\ \mathcal{P}\text{.one} & = \{C \setminus \{\mathcal{P}\text{.top}\} \mathrel{|} C \in \mathcal{P}, \mathcal{P}\text{.top} \in C\} \end{align}
が成り立ちます。
\begin{align} \mathcal{P} = \mathcal{P}\text{.zero} \cup (\mathcal{P}\text{.one} \triangleleft \mathcal{P}\text{.top}) \end{align}
が成り立ちます。逆に言えば、Diagramインスタンス
\begin{align} \mathcal{Z} = \mathcal{X} \cup (\mathcal{Y} \triangleleft v) \end{align}
が成り立つならば、
\begin{cases} \mathcal{Z}\text{.top} & := & v \\ \mathcal{Z}\text{.zero} & := & \mathcal{X} \\ \mathcal{Z}\text{.one} & := & \mathcal{Y} \end{cases} とするDiagramインスタンス として表現できます。
準備が完了したので、ここから各種演算の実装に入っていきます。
ZDDの各種演算
※ 説明文中の小文字zddは、ZDDクラスのことではなく、部分集合族を表現する本来の意味でのZDDを表します。
※ インスタンス とします。
実装する演算は以下になります：（具体例はコードにコメント文で入れてあります。）
空のzdd（
空の組合せ集合のみを持つzdd（
組合せ集合
部分集合族
部分集合族
部分集合族
部分集合族
「
1. ZDD.empty_set(self)
ZDDクラス で宣言します。0-葉がそのまま求めたいzddを表します。
def empty_set (self):
"""
空のzdd ({}) を得る。
"""
return self.zero_terminal
2. ZDD.unit_set(self)
ZDDクラス で宣言します。1-葉がそのまま求めたいzddを表します。
unitというのは、11. で定義される積の単位元 をなすことから名づけられています。
def unit_set (self):
"""
空の組合せ集合のみを持つzdd ({λ}) を得る。
"""
return self.one_terminal
3. ZDD.single_literal_set(self, v)
ZDDクラス で宣言します。下図が求めたいzddです。
def single_literal_set (self, v):
"""
組合せ集合vのみを持つzdd ({v}) を得る。
"""
assert v in self.idx
return self._get_node(v, self.zero_terminal, self.one_terminal)
4. Diagram.offset(self, v)
Diagramクラス で宣言します。
\begin{align} \mathcal{P}\text{.offset}(v) = \mathcal{P}\text{.zero} \end{align}
\begin{align} \mathcal{P}\text{.offset}(v) = \mathcal{P} \end{align}
\begin{align} & \mathcal{P}\text{.offset}(v) \\ & := \{C \in \mathcal{P} \mathrel{|} v \notin C\} \\ & = \{C \in \mathcal{P}\text{.zero} \mathrel{|} v \notin C\} \cup \{C \in (\mathcal{P}\text{.one} \triangleleft \mathcal{P}\text{.top}) \mathrel{|} v \notin C\} \\ & = \{C \in \mathcal{P}\text{.zero} \mathrel{|} v \notin C\} \cup (\{C \in \mathcal{P}\text{.one} \mathrel{|} v \notin C\} \triangleleft \mathcal{P}\text{.top}) \\ & = \mathcal{P}\text{.zero.offset}(v) \cup (\mathcal{P}\text{.one.offset}(v) \triangleleft \mathcal{P}\text{.top}) \end{align}
@ cache
def offset (self, v):
"""
selfにおいて、vを含まない組合せ集合全体をなす部分zddを得る。
例:
self := {abc, ab, c}
のとき
self.offset(c) = {ab}
"""
assert v in self.zdd.idx
if self.top == v:
return self.zero
if self.zdd.idx[self.top] > self.zdd.idx[v]:
return self
return self.zdd._get_node(self.top, self.zero.offset(v), self.one.offset(v))
5. Diagram.onset(self, v)
Diagramクラス で宣言します。
\begin{align} \mathcal{P}\text{.onset}(v) = \mathcal{P}\text{.one} \end{align}
\begin{align} \mathcal{P}\text{.onset}(v) = \{\} \end{align}
\begin{align} & \mathcal{P}\text{.onset}(v) \\ & := \{C \setminus \{v\} \mathrel{|} C \in \mathcal{P}, v \in C\} \\ & = \{C \setminus \{v\} \mathrel{|} C \in \mathcal{P}\text{.zero}, v \in C\} \cup \{ C \setminus \{v\} \mathrel{|} C \in (\mathcal{P}\text{.one} \triangleleft \mathcal{P}\text{.top}), v \in C\} \\ & = \{C \setminus \{v\} \mathrel{|} C \in \mathcal{P}\text{.zero}, v \in C\} \cup (\{ C \setminus \{v\} \mathrel{|} C \in \mathcal{P}\text{.one}, v \in C\} \triangleleft \mathcal{P}\text{.top}) \\ & = \mathcal{P}\text{.zero.onset}(v) \cup (\mathcal{P}\text{.one.onset}(v) \triangleleft \mathcal{P}\text{.top}) \end{align}
@ cache
def onset (self, v):
"""
selfにおいて、vを含む各組合せ集合からvを除いて取り出したzddを得る。
例:
self := {abc, ab, c}
のとき
self.onset(c) = {ab, λ}
"""
assert v in self.zdd.idx
if self.zdd.idx[self.top] == self.zdd.idx[v]:
return self.one
if self.zdd.idx[self.top] > self.zdd.idx[v]:
return self.zdd.zero_terminal
return self.zdd._get_node(self.top, self.zero.onset(v), self.one.onset(v))
6. Diagram.change(self, v)
Diagramクラス で宣言します。
\begin{align} \mathcal{P}\text{.change}(v) = \mathcal{P}\text{.one} \cup (\mathcal{P}\text{.zero} \triangleleft v) \end{align}
\begin{align} \mathcal{P}\text{.change}(v) = \{\} \cup (\mathcal{P} \triangleleft v) \end{align}
\begin{align} & \mathcal{P}\text{.change}(v) \\ & := \{C \setminus \{v\} \mathrel{|} C \in \mathcal{P}, v \in C\} \cup \{C \cup \{v\} \mathrel{|} C \in \mathcal{P}, v \notin C\} \\ & = (\{C \setminus \{v\} \mathrel{|} C \in \mathcal{P}\text{.zero}, v \in C\} \cup \{C \setminus \{v\} \mathrel{|} C \in (\mathcal{P}\text{.one} \triangleleft \mathcal{P}\text{.top}), v \in C\}) \\ & \cup (\{C \cup \{v\} \mathrel{|} C \in \mathcal{P}\text{.zero}, v \notin C\} \cup \{C \cup \{v\} \mathrel{|} C \in (\mathcal{P}\text{.one} \triangleleft \mathcal{P}\text{.top}), v \notin C\}) \\ & = (\{C \setminus \{v\} \mathrel{|} C \in \mathcal{P}\text{.zero}, v \in C\} \cup \{C \cup \{v\} \mathrel{|} C \in \mathcal{P}\text{.zero}, v \notin C\}) \\ & \cup ( (\{C \setminus \{v\} \mathrel{|} C \in \mathcal{P}\text{.one}, v \in C\} \cup \{C \cup \{v\} \mathrel{|} C \in \mathcal{P}\text{.one}, v \notin C\}) \triangleleft \mathcal{P}\text{.top}) \\ & = \mathcal{P}\text{.zero.change}(v) \cup (\mathcal{P}\text{.one.change}(v) \triangleleft \mathcal{P}\text{.top}) \end{align}
@ cache
def change (self, v):
"""
selfの各組合せ集合について、vが含まれて いる/いない を反転させたzddを得る。
例:
self := {abc, ab, c}
のとき
self.change(b) = {ac, a, bc}
"""
assert v in self.zdd.idx
if self.top == v:
return self.zdd._get_node(v, self.one, self.zero)
if self.zdd.idx[self.top] > self.zdd.idx[v]:
return self.zdd._get_node(v, self.zdd.zero_terminal, self)
return self.zdd._get_node(self.top, self.zero.change(v), self.one.change(v))
7. P | Q
Diagramクラス で宣言します。一方が空ならもう一方を、同じならどちらか一方を返せばよいです。
\begin{align} & \mathcal{P} \cup \mathcal{Q} \\ & = (\mathcal{P}\text{.zero} \cup (\mathcal{P}\text{.one} \triangleleft \mathcal{P}\text{.top}) ) \cup \mathcal{Q} \\ & = ( \mathcal{P}\text{.zero} \cup \mathcal{Q} ) \cup ( \mathcal{P}\text{.one} \triangleleft \mathcal{P}\text{.top}) \end{align}
\begin{align} & \mathcal{P} \cup \mathcal{Q} \\ & = \mathcal{P} \cup (\mathcal{Q}\text{.zero} \cup (\mathcal{Q}\text{.one} \triangleleft \mathcal{Q}\text{.top}) ) \\ & = (\mathcal{P} \cup \mathcal{Q}\text{.zero}) \cup (\mathcal{Q}\text{.one} \triangleleft \mathcal{Q}\text{.top}) \end{align}
\begin{align} & \mathcal{P} \cup \mathcal{Q} \\ & = (\mathcal{P}\text{.zero} \cup (\mathcal{P}\text{.one} \triangleleft \mathcal{P}\text{.top}) ) \cup (\mathcal{Q}\text{.zero} \cup (\mathcal{Q}\text{.one} \triangleleft \mathcal{P}\text{.top}) ) \\ & = (\mathcal{P}\text{.zero} \cup \mathcal{Q}\text{.zero}) \cup ( (\mathcal{P}\text{.one} \cup \mathcal{Q}\text{.one}) \triangleleft \mathcal{P}\text{.top}) \end{align}
@ cache
def __or__ (self, other):
"""
self ∪ other を表すzddを得る。
例:
self := {abc, ab, c}
other := {ab, bc, λ}
のとき
self | other = {abc, ab, bc, c, λ}
"""
assert isinstance (other, Obsolete_Diagram)
if self is self.zdd.zero_terminal:
return other
if other is self.zdd.zero_terminal or self is other:
return self
if self.zdd.idx[self.top] < self.zdd.idx[other.top]:
return self.zdd._get_node(self.top, self.zero | other, self.one)
if self.zdd.idx[self.top] > self.zdd.idx[other.top]:
return self.zdd._get_node(other.top, self | other.zero, other.one)
return self.zdd._get_node(self.top, self.zero | other.zero, self.one | other.one)
8. P & Q
Diagramクラス で宣言します。一方が空なら0-葉を、同じならどちらか一方を返せばよいです。
\begin{align} & \mathcal{P} \cap \mathcal{Q} \\ & = (\mathcal{P}\text{.zero} \cup (\mathcal{P}\text{.one} \triangleleft \mathcal{P}\text{.top}) ) \cap \mathcal{Q} \\ & = \mathcal{P}\text{.zero} \cap \mathcal{Q} \end{align}
\begin{align} & \mathcal{P} \cap \mathcal{Q} \\ & = \mathcal{P} \cap (\mathcal{Q}\text{.zero} \cup (\mathcal{Q}\text{.one} \triangleleft \mathcal{Q}\text{.top}) ) \\ & = \mathcal{P} \cap \mathcal{Q}\text{.zero} \end{align}
\begin{align} & \mathcal{P} \cap \mathcal{Q} \\ & = (\mathcal{P}\text{.zero} \cup (\mathcal{P}\text{.one} \triangleleft \mathcal{P}\text{.top}) ) \cap (\mathcal{Q}\text{.zero} \cup (\mathcal{Q}\text{.one} \triangleleft \mathcal{P}\text{.top}) ) \\ & = (\mathcal{P}\text{.zero} \cap \mathcal{Q}\text{.zero}) \cup ( (\mathcal{P}\text{.one} \cap \mathcal{Q}\text{.one}) \triangleleft \mathcal{P}\text{.top})\end{align}
@ cache
def __and__ (self, other):
"""
self ∩ other を表すzddを得る。
例:
self := {abc, ab, c}
other := {ab, bc, λ}
のとき
self & other = {ab}
"""
assert isinstance (other, Obsolete_Diagram)
if self is self.zdd.zero_terminal or other is self.zdd.zero_terminal:
return self.zdd.zero_terminal
if self is other:
return self
if self.zdd.idx[self.top] < self.zdd.idx[other.top]:
return self.zero & other
if self.zdd.idx[self.top] > self.zdd.idx[other.top]:
return self & other.zero
return self.zdd._get_node(self.top, self.zero & other.zero, self.one & other.one)
9. P + Q
Diagramクラス で宣言します。
def __add__ (self, other):
"""
（self | other と等価。）
self ∪ other を表すzddを得る。
例:
self := {abc, ab, c}
other := {ab, bc, λ}
のとき
self + other = {abc, ab, bc, c, λ}
"""
assert isinstance (other, Obsolete_Diagram)
return self.__or__(other)
10. P - Q
Diagramクラス で宣言します。
\begin{align} & \mathcal{P} - \mathcal{Q} \\ & = (\mathcal{P}\text{.zero} \cup (\mathcal{P}\text{.one} \triangleleft \mathcal{P}\text{.top}) ) - \mathcal{Q} \\ & = (\mathcal{P}\text{.zero} - \mathcal{Q}) \cup (\mathcal{P}\text{.one} \triangleleft \mathcal{P}\text{.top}) \end{align}
\begin{align} & \mathcal{P} - \mathcal{Q} \\ & = \mathcal{P} - (\mathcal{Q}\text{.zero} \cup (\mathcal{Q}\text{.one} \triangleleft \mathcal{Q}\text{.top}) ) \\ & = \mathcal{P} - \mathcal{Q}\text{.zero} \end{align}
\begin{align} & \mathcal{P} - \mathcal{Q} \\ & = (\mathcal{P}\text{.zero} \cup (\mathcal{P}\text{.one} \triangleleft \mathcal{P}\text{.top}) ) - (\mathcal{Q}\text{.zero} \cup (\mathcal{Q}\text{.one} \triangleleft \mathcal{P}\text{.top}) \\ & = (\mathcal{P}\text{.zero} - \mathcal{Q}\text{.zero}) \cup ( (\mathcal{P}\text{.one} - \mathcal{Q}\text{.one}) \triangleleft \mathcal{P}\text{.top}) \end{align}
@ cache
def __sub__ (self, other):
"""
self \ other を表すzddを得る。
例:
self := {abc, ab, c}
other := {ab, bc, λ}
のとき
self - other = {abc, c}
"""
assert isinstance (other, Obsolete_Diagram)
if self is self.zdd.zero_terminal or self is other:
return self.zdd.zero_terminal
if other is self.zdd.zero_terminal:
return self
if self.zdd.idx[self.top] < self.zdd.idx[other.top]:
return self.zdd._get_node(self.top, self.zero - other, self.one)
if self.zdd.idx[self.top] > self.zdd.idx[other.top]:
return self - other.zero
return self.zdd._get_node(self.top, self.zero - other.zero, self.one - other.one)
11. P * Q
Diagramクラス で宣言します。明らかに可換なので、一般性を失わず
\begin{align} \mathcal{P}_0 & := \mathcal{P}\text{.offset}(v) \\ \mathcal{P}_1 & := \mathcal{P}\text{.onset}(v) \\ \mathcal{Q}_0 & := \mathcal{Q}\text{.offset}(v) \\ \mathcal{Q}_1 & := \mathcal{Q}\text{.onset}(v) \end{align}
とおきます。
\begin{align} & \mathcal{P} * \mathcal{Q} \\ & = (\mathcal{P}_0 \cup (\mathcal{P}_1 \triangleleft v) ) * (\mathcal{Q}_0 \cup (\mathcal{Q}_1 \triangleleft v) ) \\ & = (\mathcal{P}_0 * \mathcal{Q}_0) \cup ( ( (\mathcal{P}_0 * \mathcal{Q}_1) \cup (\mathcal{P}_1 * \mathcal{Q}_0) \cup (\mathcal{P}_1 * \mathcal{Q}_1) ) \triangleleft v) \end{align}
@ cache
def __mul__ (self, other):
"""
「selfとotherから1つずつ取り、それらの和集合を取って得られる組合せ集合」全体を表すzddを得る。
例:
self := {ab, b, c}
other := {ab, λ}
のとき
self * other = {ab, abc, b, c}
"""
assert isinstance (other, Obsolete_Diagram)
if self.zdd.idx[self.top] > self.zdd.idx[other.top]:
return other.__mul__(self)
if other is self.zdd.zero_terminal:
return self.zdd.zero_terminal
if other is self.zdd.one_terminal:
return self
v = self.top
p0, p1 = self.offset(v), self.onset(v)
q0, q1 = other.offset(v), other.onset(v)
return self.zdd._get_node(v, p0*q0, p1*q1 + p1*q0 + p0*q1)
12. P // Q
Diagramクラス で宣言します。単位元 ）なら、（そうでなくて、）
\begin{align} \mathcal{P}_0 & := \mathcal{P}\text{.offset}(v) \\ \mathcal{P}_1 & := \mathcal{P}\text{.onset}(v) \\ \mathcal{Q}_0 & := \mathcal{Q}\text{.offset}(v) \\ \mathcal{Q}_1 & := \mathcal{Q}\text{.onset}(v) \end{align}
とおきます。
\begin{align} \mathcal{P} // \mathcal{Q} = \mathcal{P}_1 // \mathcal{Q}_1 \end{align}
\begin{align} \mathcal{P} // \mathcal{Q} = (\mathcal{P}_0 // \mathcal{Q}_0) \cap (\mathcal{P}_1 // \mathcal{Q}_1) \end{align}
@ cache
def __floordiv__ (self, other):
"""
other ≠ {} (空集合)とする。
otherの各要素Cに対し「selfのCを含む各組合せ集合からCを除いて取り出した集合全体」を取ったときの、
それらの共通部分を表すzddを得る。
例:
self := {abc, abd, ac, cd}
other := {ab, c}
のとき
self//other
= {c, d} ∩ {ab, a, d}
= {d}
"""
assert isinstance (other, Obsolete_Diagram) and other is not self.zdd.zero_terminal
if other is self.zdd.one_terminal:
return self
if self is self.zdd.zero_terminal or self is self.zdd.one_terminal:
return self.zdd.zero_terminal
if self is other:
return self.zdd.one_terminal
v = other.top
p0, p1 = self.offset(v), self.onset(v)
q0, q1 = other.offset(v), other.onset(v)
r = p1//q1
if r is not self.zdd.zero_terminal and q0 is not self.zdd.zero_terminal:
r = r & p0//q0
return r
13. P % Q
Diagramクラス で宣言します。
def __mod__ (self, other):
"""
other ≠ {} (空集合)とする。
self % other := self - other*(self/other)
例:
self := {abc, abd, ac, cd}
other := {ab, c}
のとき
self % other
= {abc, abd, ac, cd} - {ab, c}*{d}
= {abc, abd, ac, cd} - {abd, cd}
= {abc, ac}
"""
assert isinstance (other, Obsolete_Diagram) and other is not self.zdd.zero_terminal
return self - other*(self//other)
これにて、演算の実装は完了です。これらをうまく組み合わせて、様々な部分集合族に対応するZDDをボトムアップ に構築することができます。
組合せ集合の総数を求める
ZDDに含まれる組合せ集合は、根から1-葉までのパスに1対1対応します。
ということは、組合せ集合の総数を求めたければパスの総数を求めればよいということになります。DAGなので、メモ化再帰 （またはDP）でよいですね。
@ cache
def count (self):
"""
selfに含まれる組合せ集合の個数を得る。
例:
self := {abc, ab, c}
のとき
self.count() = 3
"""
if self is self.zdd.zero_terminal:
return 0
if self is self.zdd.one_terminal:
return 1
return self.zero.count() + self.one.count()
ここまで実装まとめ
import sys
sys.setrecursionlimit(1000000000 )
from pyvis.network import Network
from collections import deque
from random import randint
class Obsolete_Diagram :
def __init__ (self, zdd, top=None , zero=None , one=None ) -> None :
self.zdd = zdd
self.top = top
self.zero = zero
self.one = one
if top is None :
self.hash = randint(0 , 10 **9 )
else :
self.hash = (top, zero.hash, one.hash).__hash__()
def __hash__ (self) -> int :
return self.hash
def show (self, filename):
"""
selfによるzddを図示
filemame: html拡張子のファイル名
"""
nodes = {self: 0 }
net = Network(directed=True )
dq = deque()
if self is self.zdd.zero_terminal:
net.add_node(nodes[self], shape="box" , label="⏊" )
elif self is self.zdd.one_terminal:
net.add_node(nodes[self], shape="box" , label="⏉" )
else :
net.add_node(nodes[self], shape="circle" , label=self.top.__repr__())
dq.appendleft(self)
while dq:
p = dq.pop()
if p.zero not in nodes:
nodes[p.zero] = len (nodes)
if p.zero is self.zdd.zero_terminal:
net.add_node(nodes[p.zero], shape="box" , label="⏊" )
elif p.zero is self.zdd.one_terminal:
net.add_node(nodes[p.zero], shape="box" , label="⏉" )
else :
net.add_node(nodes[p.zero], shape="circle" , label=p.zero.top.__repr__())
dq.appendleft(p.zero)
net.add_edge(nodes[p], nodes[p.zero], color="red" )
if p.one not in nodes:
nodes[p.one] = len (nodes)
if p.one is self.zdd.zero_terminal:
net.add_node(nodes[p.one], shape="box" , label="⏊" )
elif p.one is self.zdd.one_terminal:
net.add_node(nodes[p.one], shape="box" , label="⏉" )
else :
net.add_node(nodes[p.one], shape="circle" , label=p.one.top.__repr__())
dq.appendleft(p.one)
net.add_edge(nodes[p], nodes[p.one], color="blue" )
net.show(filename, notebook=False )
@ cache
def offset (self, v):
"""
selfにおいて、vを含まない組合せ集合全体をなす部分zddを得る。
例:
self := {abc, ab, c}
のとき
self.offset(c) = {ab}
"""
assert v in self.zdd.idx
if self.top == v:
return self.zero
if self.zdd.idx[self.top] > self.zdd.idx[v]:
return self
return self.zdd._get_node(self.top, self.zero.offset(v), self.one.offset(v))
@ cache
def onset (self, v):
"""
selfにおいて、vを含む各組合せ集合からvを除いて取り出したzddを得る。
例:
self := {abc, ab, c}
のとき
self.onset(c) = {ab, λ}
"""
assert v in self.zdd.idx
if self.zdd.idx[self.top] == self.zdd.idx[v]:
return self.one
if self.zdd.idx[self.top] > self.zdd.idx[v]:
return self.zdd.zero_terminal
return self.zdd._get_node(self.top, self.zero.onset(v), self.one.onset(v))
@ cache
def change (self, v):
"""
selfの各組合せ集合について、vが含まれて いる/いない を反転させたzddを得る。
例:
self := {abc, ab, c}
のとき
self.change(b) = {ac, a, bc}
"""
assert v in self.zdd.idx
if self.top == v:
return self.zdd._get_node(v, self.one, self.zero)
if self.zdd.idx[self.top] > self.zdd.idx[v]:
return self.zdd._get_node(v, self.zdd.zero_terminal, self)
return self.zdd._get_node(self.top, self.zero.change(v), self.one.change(v))
@ cache
def __or__ (self, other):
"""
self ∪ other を表すzddを得る。
例:
self := {abc, ab, c}
other := {ab, bc, λ}
のとき
self | other = {abc, ab, bc, c, λ}
"""
assert isinstance (other, Obsolete_Diagram)
if self is self.zdd.zero_terminal:
return other
if other is self.zdd.zero_terminal or self is other:
return self
if self.zdd.idx[self.top] < self.zdd.idx[other.top]:
return self.zdd._get_node(self.top, self.zero | other, self.one)
if self.zdd.idx[self.top] > self.zdd.idx[other.top]:
return self.zdd._get_node(other.top, self | other.zero, other.one)
return self.zdd._get_node(self.top, self.zero | other.zero, self.one | other.one)
@ cache
def __and__ (self, other):
"""
self ∩ other を表すzddを得る。
例:
self := {abc, ab, c}
other := {ab, bc, λ}
のとき
self & other = {ab}
"""
assert isinstance (other, Obsolete_Diagram)
if self is self.zdd.zero_terminal or other is self.zdd.zero_terminal:
return self.zdd.zero_terminal
if self is other:
return self
if self.zdd.idx[self.top] < self.zdd.idx[other.top]:
return self.zero & other
if self.zdd.idx[self.top] > self.zdd.idx[other.top]:
return self & other.zero
return self.zdd._get_node(self.top, self.zero & other.zero, self.one & other.one)
def __add__ (self, other):
"""
（self | other と等価。）
self ∪ other を表すzddを得る。
例:
self := {abc, ab, c}
other := {ab, bc, λ}
のとき
self + other = {abc, ab, bc, c, λ}
"""
assert isinstance (other, Obsolete_Diagram)
return self.__or__(other)
@ cache
def __sub__ (self, other):
"""
self \ other を表すzddを得る。
例:
self := {abc, ab, c}
other := {ab, bc, λ}
のとき
self - other = {abc, c}
"""
assert isinstance (other, Obsolete_Diagram)
if self is self.zdd.zero_terminal or self is other:
return self.zdd.zero_terminal
if other is self.zdd.zero_terminal:
return self
if self.zdd.idx[self.top] < self.zdd.idx[other.top]:
return self.zdd._get_node(self.top, self.zero - other, self.one)
if self.zdd.idx[self.top] > self.zdd.idx[other.top]:
return self - other.zero
return self.zdd._get_node(self.top, self.zero - other.zero, self.one - other.one)
@ cache
def __mul__ (self, other):
"""
「selfとotherから1つずつ取り、それらの和集合を取って得られる組合せ集合」全体を表すzddを得る。
例:
self := {ab, b, c}
other := {ab, λ}
のとき
self * other = {ab, abc, b, c}
"""
assert isinstance (other, Obsolete_Diagram)
if self.zdd.idx[self.top] > self.zdd.idx[other.top]:
return other.__mul__(self)
if other is self.zdd.zero_terminal:
return self.zdd.zero_terminal
if other is self.zdd.one_terminal:
return self
v = self.top
p0, p1 = self.offset(v), self.onset(v)
q0, q1 = other.offset(v), other.onset(v)
return self.zdd._get_node(v, p0*q0, p1*q1 + p1*q0 + p0*q1)
@ cache
def __floordiv__ (self, other):
"""
other ≠ {} (空集合)とする。
otherの各要素Cに対し「selfのCを含む各組合せ集合からCを除いて取り出した集合全体」を取ったときの、
それらの共通部分を表すzddを得る。
例:
self := {abc, abd, ac, cd}
other := {ab, c}
のとき
self//other
= {c, d} ∩ {ab, a, d}
= {d}
"""
assert isinstance (other, Obsolete_Diagram) and other is not self.zdd.zero_terminal
if other is self.zdd.one_terminal:
return self
if self is self.zdd.zero_terminal or self is self.zdd.one_terminal:
return self.zdd.zero_terminal
if self is other:
return self.zdd.one_terminal
v = other.top
p0, p1 = self.offset(v), self.onset(v)
q0, q1 = other.offset(v), other.onset(v)
r = p1//q1
if r is not self.zdd.zero_terminal and q0 is not self.zdd.zero_terminal:
r = r & p0//q0
return r
def __mod__ (self, other):
"""
other ≠ {} (空集合)とする。
self % other := self - other*(self/other)
例:
self := {abc, abd, ac, cd}
other := {ab, c}
のとき
self % other
= {abc, abd, ac, cd} - {ab, c}*{d}
= {abc, abd, ac, cd} - {abd, cd}
= {abc, ac}
"""
assert isinstance (other, Obsolete_Diagram) and other is not self.zdd.zero_terminal
return self - other*(self//other)
@ cache
def count (self):
"""
selfに含まれる組合せ集合の個数を得る。
例:
self := {abc, ab, c}
のとき
self.count() = 3
"""
if self is self.zdd.zero_terminal:
return 0
if self is self.zdd.one_terminal:
return 1
return self.zero.count() + self.one.count()
class ZDD :
def __init__ (self, ground_set, Diagram=Obsolete_Diagram) -> None :
self.idx = {v: i for i, v in enumerate (ground_set)}
self.idx[None ] = len (ground_set)
self.Diagram = Diagram
self.zero_terminal = self.Diagram(zdd=self)
self.one_terminal = self.Diagram(zdd=self)
@ cache
def _get_node (self, v, zero, one):
if one is self.zero_terminal:
return zero
return self.Diagram(self, v, zero, one)
def empty_set (self):
"""
空のzdd ({}) を得る。
"""
return self.zero_terminal
def unit_set (self):
"""
空の組合せ集合のみを持つzdd ({λ}) を得る。
"""
return self.one_terminal
def single_literal_set (self, v):
"""
組合せ集合vのみを持つzdd ({v}) を得る。
"""
assert v in self.idx
return self._get_node(v, self.zero_terminal, self.one_terminal)
最後に、これらのZDD演算を利用して解ける有名な数え上げの問題を1つ紹介します。
エイト・クイーン - Wikipedia
8×8のチェス盤に、相互に攻撃が当たらないようクイーンを8個配置する方法は何通り？と言う問題です。
配置方法の1例（エイト・クイーン - Wikipedia ）より
この問題は「各マスを台集合とし、クイーンを配置するマスを部分集合として取り出す」と捉えることで、解全体をZDDを用いて表現することができます。
8-Queen problem の解全体を表すZDDの構築方法
各行にはクイーンを1つ配置するので、上の行から順にどの列にクイーンを配置するかを決めていきながら、その行までで考えられる配置全体を表すZDDを構築していきます。マス
このマスにクイーンを配置できるのは上と斜め上の各マスにクイーンが置かれていないときに限るので、
つまり、それぞれのマスについて
〇 のマスを含まない組合せ集合を
実装例
8×8のチェス盤に限る必要はないので、一般のn×nのチェス盤で解けるようにしました。solve() を show = True で実行すればZDDを図示してくれます。
class QueenProblem :
def solve (n: int , show: bool = False ) -> int :
"""
n×n チェス盤でのクイーン問題を解く。
show: zddを表示するか ->
"""
assert type (n) is int and 1 <= n
def grid (i, j):
return i*n + j
zdd = ZDD([grid(i, j) for i in range (n) for j in range (n)])
s = zdd.empty_set()
for j in range (n):
s += zdd.single_literal_set(j)
for i in range (1 , n):
t = zdd.empty_set()
for j in range (n):
u = s
for k in range (i):
u = u.offset(grid(i-k-1 , j))
for k in range (min (i, j)):
u = u.offset(grid(i-k-1 , j-k-1 ))
for k in range (min (i, n-j-1 )):
u = u.offset(grid(i-k-1 , j+k+1 ))
t += u.change(grid(i, j))
s = t
if show:
s.show(f" Queen_problem{n}.html" )
return s.count()
n = 8 での ZDD
nごとの実行時間
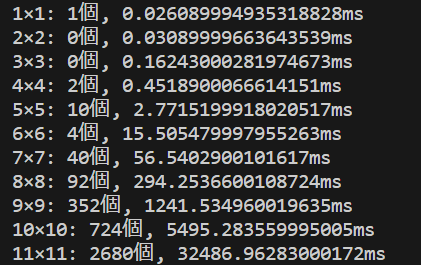
せっかくなので、私の環境でどれくらいの速度で n-Queen problem が解けたかの記録を残しておきます。各nごとに10回の平均を取ります。
from time import perf_counter
def timer_return_time (func):
"""
関数の実行時間を計測するwrapper
実行時間(ms)を返り値に追加する
"""
def wrapper (*arg, **darg):
begin = perf_counter()
ret = func(*arg, **darg)
end = perf_counter()
return ret, (end-begin)*1000
return wrapper
class QueenProblem :
@ timer_return_time
def solve (n: int , show: bool = False ) -> int :
(中略)
return s.count()
if __name__ == "__main__" :
repeat = 10
for n in range ( 11 , 12 ):
t = 0
for _ in range (repeat):
ans, time = QueenProblem.solve(n, False )
t += time
print (f "{n}×{n}: {ans}個, {t/repeat}ms" ) 実行環境：
Python 3.11.4 (tags/v3.11.4:d2340ef, Jun 7 2023, 05:45:37) [MSC v.1934 64 bit (AMD64 )] on win32windows 11Intel (R) Core(TM) i7-10510U CPU @ 1.80GHz 2.30 GHz8.00 GB
実行結果：
n = 1 ~ 11 での実行結果。n = 12 はしばらく待っても終わりませんでした。
※ ちなみにバックトラックした方が普通に速いらしい です。
Nクイーン【前編】 | TECH PROjin
おわりに
お読みいただきありがとうございました。
卒研お勉強枠次回は、ZDDを使って某有名パズルゲーム を解くお話になる予定です。気長にお待ちください。
次回 >>
参考文献
[1] Zero-suppressed BDDs and their applications (湊真一)
[2] 超高速グラフ列挙アルゴリズム｜森北出版株式会社 (ERATO 湊離散構造処理系プロジェクト 著, 湊真一 編)
[3] ZDD (Zero-suppressed binary Decision Diagram) 超高速グラフ列挙アルゴリズム 著者: 湊 真一 (石井 健太)
[4] エイト・クイーン - Wikipedia
[5] Nクイーン【前編】 | TECH PROjin
