【Trie木】ABC377G - Edit to Match の図説
この記事でやること
ABC377G-Edit to Match の図説です。やってることは公式解説と同じです。
解法
便宜上 を空文字列として、
まで処理済みで
を
したTrie木を考えます。(Trie木を知らない方は、参考文献に記載した記事などを参照してください。)
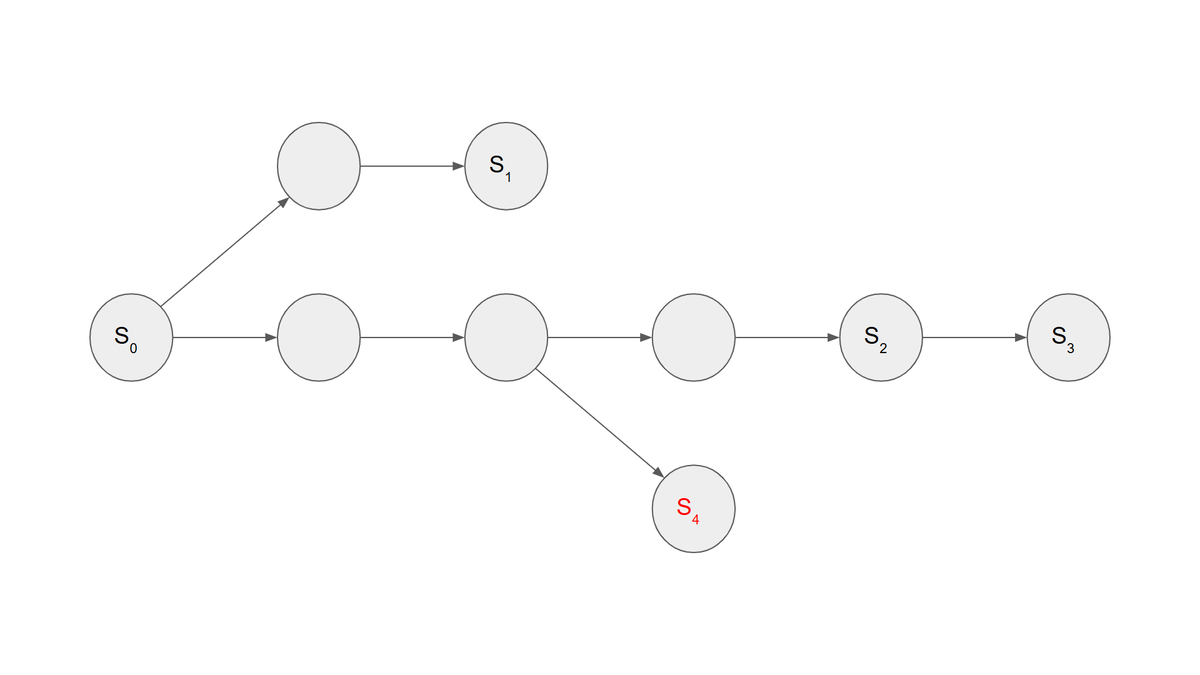
ここで、 に対する解は
になります。上図の場合、
から
または
が最短で、答えは
になります。
これは、各ノード について
を記録しておくことで高速に解くことができます。
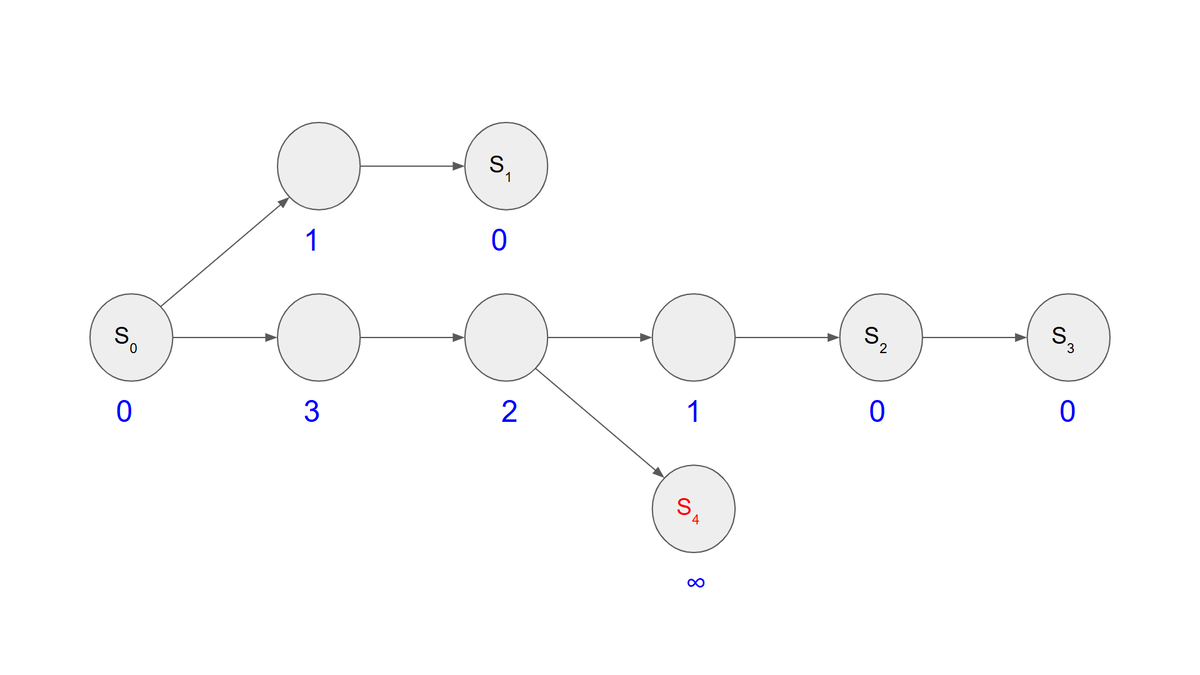
Trie木の根から のノードまでのパスを
としたとき、求める解は
となります。
また、 は
の帰りがけにchminすることで簡単に更新できますね。
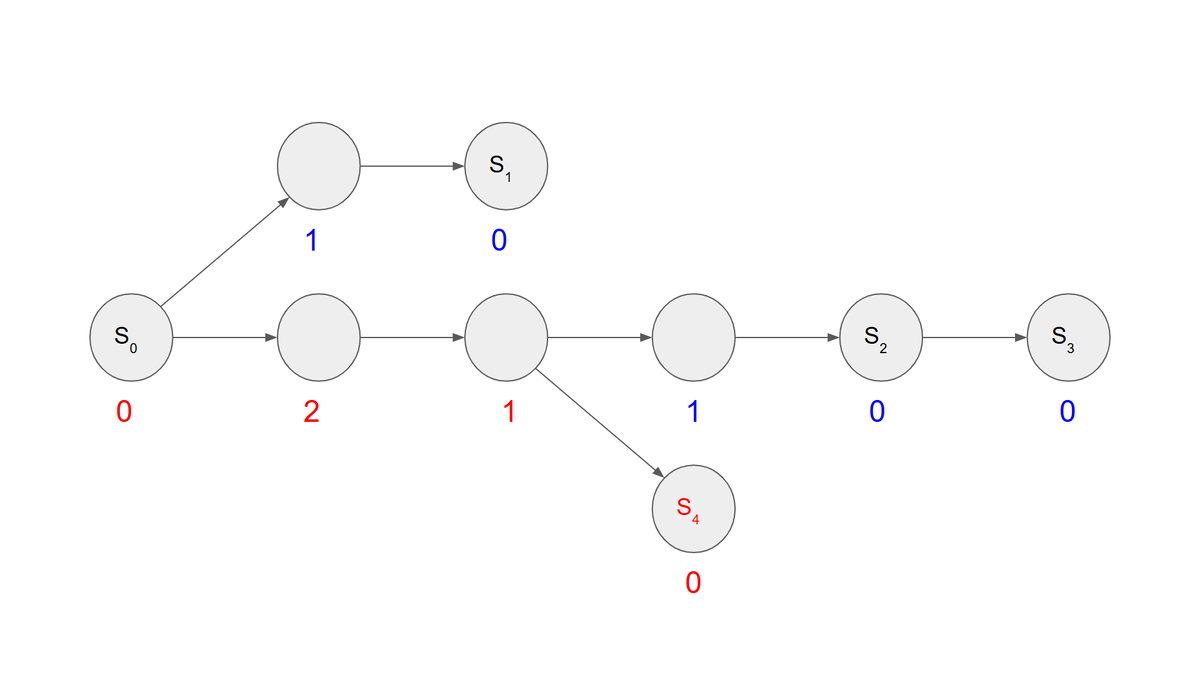
計算量は、各文字列 に対し
*1 になります。
提出コード
Python (PyPy 3.10-v7.3.12)
Submission #59196277 - TOYOTA SYSTEMS Programming Contest 2024(AtCoder Beginner Contest 377)
おわりに
公式解説、こういう挿絵とかあったらもっとわかりやすいのにね…。
参考文献
トライ木(Trie木) の解説と実装【接頭辞(prefix) を利用したデータ構造】 | アルゴリズムロジック
*1:Trie木の枝をhashmapで持った場合の期待計算量。配列で持つなら文字種数σ倍が付きます。