【ABC388-G 解説?】並列二分探索に裏切られた話
はじめに
前回の記事 で並列二分探索というテクニックについて触れましたが、ABC388 にてついに並列二分探索の出番が来たので早速試してきました!
この記事でやること
-
G - Simultaneous Kagamimochi 2 の並列二分探索解法の解説
問題概要
個の餅がサイズの昇順に並んでおり、各餅
のサイズは
である。(つまり、各
について
)
個の質問に答える。各質問
の内容は次の通り:
- 実行時間制限: 2sec
なお、各クエリは E問題 に相当します。
各クエリについての自然な発想として、以下のような貪欲法が浮かびます:
- 上の餅を昇順に見る。
- 1.の餅に対して、「まだ使っていない餅であって、下の餅として採用できる最小の餅」とマッチングさせる。
しかし、残念ながらこれは次のようなケースで壊れます。悲しい。
\begin{equation} A = [1, 2, 3, 4] \end{equation}
というわけで、各クエリだけでも解法をちゃんと考えなくてはなりません。
解法解説
クエリごとの解法について
作る鏡餅の個数を決め打ち二分探索すればよいです。
すなわち、 個の鏡餅を作れるか?という判定問題を考えると、小さい餅上位
個と大きい餅上位
個について、小さい順にマッチングさせられるか を見ればよいです。
つまり、各判定問題は で解けます。
※ 正当性の説明については E問題の公式解説 を参照してください
判定問題を並列に解く
前節での決め打ち二分探索を各クエリごとに行うと、全体 となり間に合いません。
前回の記事 でも解説した通り、並列二分探索は 個の判定問題を並列して解くことで高速化します。
各クエリ ごとに
個の鏡餅を作れるか?という判定問題を考え、並列に解く方法を考えます。
上側に置く餅を昇順に走査します。
このとき、前節での判定問題の解法によると、各クエリについて、マッチング相手として見るべき餅は1つだけです。
また、餅がサイズの昇順に並んでいることに注意すると、クエリを「今見ている上側の餅のindexからマッチング相手のindexまでの距離」*1で昇順にソートしてある時、マッチング相手としてよいかの判定結果に単調性が現れます。
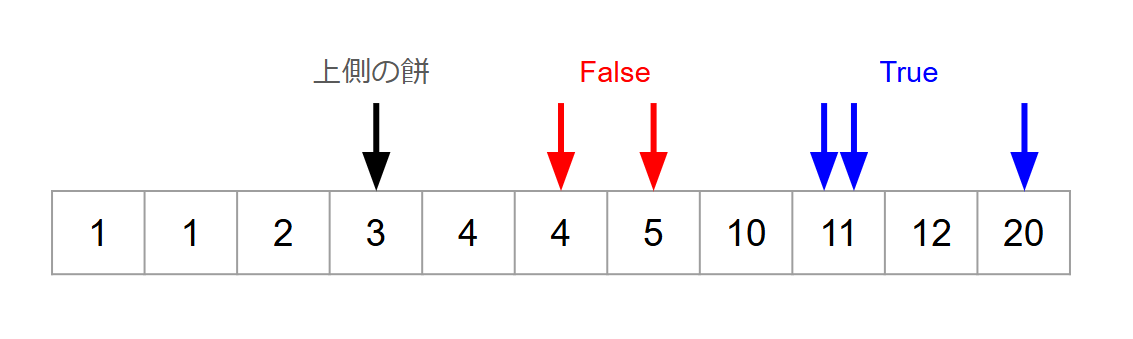
一度 False と判定されたクエリはその時点で 個の鏡餅が作れないことが確定するので、以降は考えなくてよいです。

以上を踏まえると、
- 上側の餅を走査しつつ、
- イベントソートによって判定するクエリを「今見ている上側の餅のindexからマッチング相手のindexまでの距離」の昇順に持ち、
- 「持っているクエリのうち先頭にあるもののマッチング相手が False になるならそのクエリの判定結果を False として捨てる」を while文 で処理
の要領で、 個の判定問題を並列して解くことができます。
クエリの持ち方としては、最小ヒープを使えばよいです。イベント終了の処理は 遅延評価 で行えばよいです。
計算量は です。
実装例
TLEしました笑。
おわりに
いかがでしたか?
TL が 2sec な時点で嫌な予感がしていたのですが、案の定でした。悲しい…
PyPyで通る気は今のところしていないのですが、高速な言語だと通ったりするんですかね。
最後までお読みいただきありがとうございました。
PyPyでもちゃんと通る解法(2024/1/15 追記)
各餅に対し「初めてサイズが2倍以上になる餅までの距離(存在しない場合は∞)」を並べた配列を二分探索や尺取法などで作成しておき、これを Range Max が で取れるデータ構造(Sparse Table 等)に載せておくことで、各クエリの決め打ち二分探索が
で解けるようです*2。何故気が付かなかったのか…。